حل اسئلة اختبار منتصف الفصل الخامس
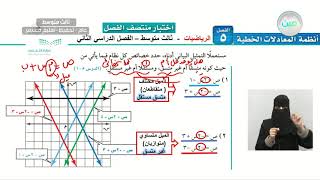
مستعملاً التمثيل البياني أدناه، حدد خصائص كل نظام فيما يأتي من حيث كونه متسقاً أم غير متسق، ومستقلاً أم غير مستقل:
١) ص = ٢س - ١
ص = -٢س + ٣
بما أن الخطين الممثلين للمعادلتين متقاطعين في نقطة إذاً متسق ومستقل.
٢) ص = -٢س + ٣
ص = -٢س - ٣
بما أن الخطين الممثلين للمعادلتين متوازيين إذاً النظام غير متسق.
مثل كل نظام فيما يأتي بيانياً، وأوجد عدد حلوله، وإن كان واحداً فاكتبه:
٣) ص = ٢س - ٣
ص = س + ٤
لها حل واحد هو (٧، ١١)
متسق ومستقل.
٤) س + ص = ٦
س - ص = ٤
لها حل واحد وهو (٥، ١)
٥) س + ص = ٨
٣س + ٣ص = ٢٤
لها عدد لا نهائي من الحلول متسق وغير مستقل.
٦) س - ٤ص = -٦
ص = -١
لا يوجد حل، غير متسق.
٧) ٣س + ٢ص = ١٢
٣س + ٢ص = ٦
لا يوجد حل، غير متسق.
٨) ٢س + ص = -٤
٥س + ٣ص = -٦
لها حل واحد وهو (-٦، ٨)
متسق، ومستقل.
حل كلاً من الأنظمة مستعملاً التعويض:
٩) ص = س + ٤
٢س + ص = ١٦
بالتعويض عن ص في المعادلة الثانية:
٢س + (س + ٤) = ١٦
٢س + س + ٤ = ١٦
٣س = ١٢
س = ٤
بالتعويض عن س
ص = ٤ + ٤ = ٨
ص = ٨
حل النظام هو (٤، ٨)
١٠) ص = -٢س - ٣
س + ص = ٩
بالتعويض عن ص في المعادلة الثانية:
س + (-٢س - ٣) = ٩
س - ٢س - ٣ = ٩
- س = ١٢
س = -١٢
بالتعويض س = -١٢
ص = -٢(-١٢ + ٣) = ١٨
ص = ١٨
حل النظام هو (-١٢، ١٨)
١١) س + ص = ٦
س - ص = ٨
من المعادلة الثانية س = ص + ٨
بالتعويض في المعادلة الأولى:
(ص + ٨) + ص = ٦
ص + ٨ + ص = ٦
٢ص = -٢
ص = -١
بالتعويض عن ص
س = -١ + ٨
س = ٧
حل النظام هو (٧، -١)
١٢) ص = -٤س
٦س - ص = ٣٠
بالتعويض عن ص في المعادلة الثانية:
٦س -(-٤س) = ٣٠
٦س + ٤س = ٣٠
١٠س = ٣٠
س = ٣
بالتعويض عن س في المعادلة الأولى:
ص = -٤ × ٣
ص = -١٢
حل النظام هو (٣، -١٢)
١٣) حديقة الحيوان: الجدول الآتي يبين، تكلفة دخول عائلتين لحديقة الحيوان في إحدى المدن.
| العائلة | المجموعة | التكلفة الإجمالية |
| أ | ٤كبار وطفلان | ١٨٤ ريالاً |
| ب | ٤كبار و٣ أطفال | ٢٠٠ ريال |
أ) عرف المتغيرات التي تمثل ثمن التذكرة للكبار وثمن التذكرة للأطفال.
افرض س هي ثمن تذكرة الكبار، ص ثمن تذكرة الأطفال.
ب) اكتب نظاماً من معادلتين لإيجاد ثمن كل من تذكرتي الكبار والأطفال.
- ٤س + ٢ص = ١٨٤
- ٤س + ٣ص = ٢٠٠
جـ) حل النظام، ووضح ماذا يعني الحل.
بطرح المعادلتين ص = ١٦
بالتعويض في المعادلة الأولى:
٤س + ٣٢ = ١٨٤
س = ٧٦
يعني أن ثمن تذكرة الكبار ٧٦ ريال.
وثمن تذكرة الأطفال ١٦ ريال.
د) ما تكلفة دخول مجموعة مكونة من ٣كبار و٥ أطفال لحديقة الحيوان؟
- تكلفة دخول الكبار = ٣ × ٧٦ = ٢٢٨ ريال.
- تكلفة دخول الأطفال = ٥ × ١٦ = ٨٠ ريال.
- تكلفة الدخول = ٢٢٨ + ٨٠ = ٣٠٨ ريال.
١٤) اختيار من متعدد: تريد أسماء ١٢ قطعة من الشوكولاتة والمصاص؛ إذا كان مع أسماء ١٦ ريالاً، وكان ثمن قطعة الشوكولاتة ريالين، وثمن قطعة المصاص ريالاً، فكم قطعة من كل نوع ستشتري؟
أ) ٦ قطع شوكولاتة، ٦ قطع مصاص.
ب) ٤ قطع شوكولاتة، ٨ قطع مصاص.
جـ) ٧ قطع شوكولاتة، ٥ قطع مصاص.
د) ٣ قطع شوكولاتة، ٩ قطع مصاص.
حل كلاً من أنظمة المعادلات الآتية مستعملاً طريقة الحذف:
١٥) س + ص = ٩
س - ص = -٣
بجمع المعادلتين:
٢س = ٦
س = ٣
بالتعويض عن س في المعادلة الأولى:
٣ + ص = ٩
ص = ٦
حل النظام هو (٣، ٦)
١٦) س + ٣ص = ١١
س + ٧ص = ١٩
بطرح المعادلة الأولى من المعادلة الثانية:
٤ص = ٨
ص = ٢
بالتعويض عن ص في المعادلة الأولى:
س + ٦ = ١١
س = ٥
حل النظام هو (٥، ٢)
١٧) ٩س - ٤ص = -٦
٣س + ٤ص = ١٠
بقسمة المعادلة الأولى على ٣
٣س - ٨ص = - ٢ ٣
بطرح المعادلة ٣ من المعادلة ٢
١٢ص = ١٢
ص = ١
بالتعويض عن ص في المعادلة ٢
٣س + ٤ × ١ = ١٠
٣س = ٦
س = ٢
حل النظام هو (٢، ١)
١٨) -٥س +٢ص = -١١
٥س -٧ص = ١
بجمع المعادلتين
-٥ص = -١٠
ص = ٢
بالتعويض عن ص في المعادلة الثانية:
٥س - ٧ × ٢ = ١
٥س = ١٥
س = ٣
حل النظام هو (٣، ٢)
حلول أسئلة الصف الثالث المتوسط
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى



.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات