حل أسئلة تدرب وحل المسائل
إذا كانت م = ٢، ن = ١٦، فاحسب قيمة كل عبارة مما يأتي:
٨) م + ١٠
٢ + ١٠ = ١٢
٩) ن + ٨
١٦ + ٨ = ٢٤
١٠) ٩ - م
٩ - ٢ = ٧
١١) ٢٢ - ن
٢٢ - ١٦ = ٦
١٢) ن ÷ ٤
١٦ ÷ ٤ = ٤
١٣) ١٢ ÷ م
١٢ ÷ ٢ = ٦
١٤) ن × ٣
١٦ × ٣ = ٤٨
١٥) ٦م
٦(٢) = ١٢
١٦) م + ن
٢ + ١٦ = ١٨
١٧) ن + م
١٦ + ٢ = ١٨
١٨) ن - ٦
١٦ - ٦ = ١٠
١٩) م - ١
٢ - ١ = ١
إذا كانت أ = ٤، ب = ٧، جـ = ١١، فاحسب قيمة كل عبارة مما يأتي:
٢٠) ب - أ
٧ - ٤ = ٣
٢١) جـ - ب
١١ - ٧ = ٤
٢٢) ٥جـ + ٦
٥(١١) + ٦
= ٥٥ + ٦
= ٦١
٢٣) ٢ب + ٧
٢(٧) + ٧
= ١٤ + ٧
= ٢١
٢٤) ٣أ - ٤
٣(٤) - ٤
= ١٢ - ٤
= ٨
٢٥) ٤ب - ١٠
٤(٧) - ١٠
= ٢٨ - ١٠
= ١٨
٢٦) نبتة الخيزران: تستعمل العبارة ن لإيجاد مقدار نمو نبتة معينة من الخيزران في زمن محدد؛ حيث تدل م على معدل النمو، وتدل ن على مقدار الزمن، فما مقدار النمو لهذه النبتة في ٧ ايام إذا كان معدل نموها ٩٠ سنتمتراً في اليوم الواحد؟
م ن = (٩٠) (٧) = ٦٣٠ سم.
٢٧) سباق: تستعمل العبارة ف ÷ ن لإيجاد معدل السرعة؛ حيث ف المسافة المقطوعة، وتمثل ن الزمن، أوجد السرعة ع لسيارة سباق قطعت ٨١٢ كلم في ٤ ساعات.
ع = ف ÷ ن = ٨١٢ ÷ ٤ = ٢٠٣ كلم/ساعة.
إذا كانت أ = ٩، ب = ١٥، س = ٣، ع = ٨، فاحسب قيمة كل عبارة مما يأتي:
٢٨) ب٢ - ٥أ
= (١٥)٢ - ٥(٩) = ٢٢٥ - ٤٥ = ١٨٠
٢٩) ٤ب ÷ ٥
٤(١٥) ÷ ٥ = ٦٠ ÷ ٥ = ١٢
٣٠) ٢أ ب
٢ (٩) (١٥) = ٢٧٠
٣١) ٤ع + ٨ - ٦
٤(٨) + ٨ - ٦
= ٣٢ + ٨ - ٦
= ٤٠ - ٦
= ٣٤
٣٢) ٧ع ÷ ٤ + ٥س
٧(٨) ÷ ٤ + ٥(٣)
= ٥٦ ÷ ٤ + ٥ × ٣
= ١٤ + ٥ × ٣
= ١٤ + ١٥
= ٢٩
٣٣) ع٢ - (٥س)
(٨)٢ - (٥ × ٣)
= ٦٤ - ١٥
= ٤٩
٣٤) طائرات: تستعمل العبارة ٩٠٠ن؛ لحساب المسافة بالكيلومترات التي تقطعها طائرة (البوينغ ٧٨٧)؛ حيث يمثل المتغير ن الزمن بالساعات، أوجد المسافة التي تقطعها هذه الطائرة في زمن مقداره ٤ ساعات.
ف = ٩٠٠ن
ف = ٩٠٠ × ٤
= ٣٦٠٠ كلم.
٣٥) هندسة: نستعمل العبارة ل ع لحساب مساحة المستطيل؛ حيث يمثل ل الطول، ع العرض، احسب مساحة المستطيل المجاور؟
ل ع = ١٦ × ٧ = ١١٢ سم٢.
٣٦) تحد: أدخل محمد العدد ١٠٠ في آلته الحاسبة، ثم طرح ٧ عدة مرات، بينما بدأ عبد القادر من الصفر، ثم أخذ يضيف ٣ في كل مرة، فإذا كان الاثنان يقومان بعملية واحدة كل مرة، فهل سيصلان إلى العدد نفسه؟ إذا كانت الإجابة نعم، فما هذا العدد؟ فسر لإجابتك.
| محمد | ١٠٠ | ٩٣ | ٨٦ | ٧٩ | ٧٢ | ٦٥ | ٥٨ | ٥١ | ٤٤ | ٣٧ | ٣٠ |
| عبد القادر | ٠ | ٣ | ٦ | ٩ | ١٢ | ١٥ | ١٨ | ٢١ | ٢٤ | ٢٧ | ٣٠ |
٣٧) اختر طريقة: يريد سالم إيجاد قيمة س٢ - ص، عندما س = ٣، ص = ٨، فأي الطرق الآتية يستعملها لإيجاد قيمة العبارة؟ علل اختيارك، ثم استعملها لحل المسألة.
الحساب الذهني؛ يمكن لسالم حساب قيمة س٢ ذهنياً ثم يطرح قيمة س٢
ص = ٩ - ٨ = ١
٣٨) اكتشف المختلف: حدد العبارة المختلفة عن العبارات الثلاث الأخرى، وفسر إجابتك.
٦ + ٨؛ لا تحتوي متغيرات.
٣٩) اكتب قارن بين العبارات العددية والعبارات الجبرية، استعمل أمثلة توضيحية.
تستعمل كلتا العبارتين العددية والجبرية في العمليات.
ومثال ذلك ٦ + ٧، ٦ + أ وتتضمن العبارة الجبرية أعداداً أو متغيرات على حين تتضمن العبارة العددية أعداداً فقط مثال ذلك ٣س أو ٧ × ٣
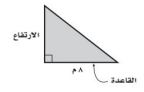
٤٠) يمكن إيجاد ارتفاع المثلث أدناه باستعمال العبارة ٤٨ ÷ ب، حيث ب تمثل قاعدة المثلث، أوجد ارتفاع المثلث.
أ) ٤م.
ب) ٦م.
جـ) ٨م.
د) ١٠م.
٤١) يبين الجدول أدناه مجموع الميداليات التي حصلت عليها بعض الدول المشاركة في دورة الألعاب الأولمبية الشتوية عام ٢٠١٤م.
| الدولة | مجموع الميداليات |
| ألمانيا | ١٩ |
| أمريكا | ٢٨ |
| كندا | س |
| هولندا | ٢٤ |
| روسيا | ٣٣ |
| النرويج | ٢٦ |
أي عبارة مما يأتي تمثل المجموع الكلي للميداليات في الجدول؟
أ) ١٣٠ - س
ب) ٢س + ١٣٠
جـ) س - ١٣٠
د) ١٣٠ + س
٤٢) إجابة قصيرة: إذا كان ٤س يمثل محيط مربع طول ضلعه س، فأوجد محيط مربع طول ضلعه ٢٦ سم.
محيط المربع = ٤ × طول الضلع.
بما أن طول الضلع = ٢٦ سم.
إذاً محيط المربع = ٤ × ٢٦ = ١٠٤ سم.
حلول أسئلة الصف السادس الابتدائي
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)



النقاشات