حلول الأسئلة
السؤال
وضح العلاقة بين المثلثات ونظرية مجموع قياسات الزوايا الداخل للمضلع.
الحل
اشتُقت نظرية مجموع قياسات الزوايا الداخلية للمضلع من النمط الذي يربط عدد أضلاع المضلع بعدد المثلثات والصيغة هي حاصل ضرب مجموع قياسات زوايا المثلث أي 180º في عدد المثلثات في المضلع.
شاهد حلول جميع الاسئلة
مسائل مهارات التفكير العليا

43) اكتشف الخطأ: قالت مريم: إن مجموع قياسات الزوايا الخارجية للعشاري أكبر منه للسباعي لأن عدد أضلاع العشاري أكثر من أضلاع السباعي وقالت لبنى: إن مجموع قياسات الزوايا الخارجية لكل المضلعين متساوي "فهل أي منهما ادعاؤها صحيح"؟ وضح تبريرك.
الحل:
لبنى؛ حسب نظرية مجموع قياسات الزوايا الخارجية سيكون مجموع قياسات الزوايا الخارجية لأي مضلع يساوي 360.
44) تحدٍ: أوجد قيم c, b, a في الشكل السداسي المنتظم QRSTVX المجاور وبرر اجابتك .
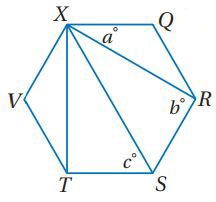
الحل:
60 , 90 , 30؛ حسب نظرية مجموع قياسات الزوايا الداخلية يكون مجموع قياسات الزوايا الداخلية 720 وبما أن المضلع QRSTVX منتظم فإن له 6 زوايا متطابقة وقياس كل زاوية 120 لذلك.
وكذلك XQ = QR
وحسب نظرية المثلث متطابق الضلعين يكون.
وبما أن مجموع قياسات الزوايا الداخلية للمثلث 180º فإن:
وبناءاً على مسلمة جمع الزوايا يكون:
وبالتعويض:
إذن وبما أن:
ولأن العناصر المتناظرة في المثلثين المتطابقين متطابقة فإن
وفي
وبالتعويض إذن
45) تبرير: إذا مد ضلعان لسداسي منتظم بحيث يلتقيان في نقطة خارجه فهل يكون المثلث الناتج متطابق الأضلاع دائماً أو أحياناً أو لا يمكن أن يكون متطابق الأضلاع أبداً؟ برر اجابتك.
الحل:
دائماً؛ حسب نظرية مجموع الزوايا الخارجية.
ولما كان مجموع قياسات الزوايا الداخلية لأي ضلع مثلث يساوي 180º فإن:
إذن فالمثلث متطابق الأضلاع.
46) مسألة مفتوحة: ارسم مضلعاً وأوجد مجموع قياسات زواياه الداخلية.
ما عدد أضلاع المضلع الذي مجموع قياسات زواياه الداخلية مثل المجموع الذي أوجدته؟ برر اجابتك.
الحل:
مجموع قياسات الزوايا الداخلية لهذا المضلع يساوي.
ومثلاً هذا المجموع يساوي (540).2 أو 1080
وعدد أضلاع المضلع الذي مجموع قياسات زواياه الداخلية 1080º
وهو حل المعادلة ومنها 8 = n.
47) اكتب: وضح العلاقة بين المثلثات ونظرية مجموع قياسات الزوايا الداخل للمضلع.
الحل:
اشتُقت نظرية مجموع قياسات الزوايا الداخلية للمضلع من النمط الذي يربط عدد أضلاع المضلع بعدد المثلثات والصيغة هي حاصل ضرب مجموع قياسات زوايا المثلث أي 180º في عدد المثلثات في المضلع.
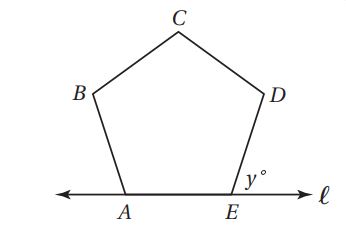
48) إجابة قصيرة: الشكل ABCDE خماسي منتظم والمستقيم يحوي ما قياس ()
الحل:
49) إذا كان مجموع قياسات الزوايا الداخلية لمضلع مثلي مجموع قياسات زواياه الخارجية فما نوع هذا المضلع؟
- مربع.
- خماسي.
- سداسي.
- ثماني.