حلول الأسئلة
السؤال
حدد ما إذا كان كلّ زوج من الزوايا الآتية متكاملة أو متتامّة أو غير ذلك.
الحل
مجموع الزاويتان = ٩٠ + ٤٣ = ١٣٣
إذاً الزاويتان غير متتامتان وغير متكاملتان.
مجموع الزاويتان = ٦١ + ١١٩ = ١٨٠
إذاً الزاويتان متكاملتان.
مجموع الزاويتان = ٩٠ + ٩٠ = ١٨٠
إذا الزاويتان متكاملتان.
بما أن مجموع الزاويتان ١٨٠
إذاً الزاويتان متكاملتان.
بما أن مجموع الزاويتان ٩٠
إذاً الزاويتان متتامتان.
بما أن مجموع الزاويتان أكبر من ٩٠ وأقل من ١٨٠
إذاً الزاويتان غير متكاملتان وغير متتامتان.
شاهد حلول جميع الاسئلة
حل اسئلة تدرب وحل المسائل
حدد ما إذا كان كل زوج من الزوايا الآتية متكاملة أو متتامة أو غير ذلك.
٤) .JPG)
مجموع الزاويتان = ٩٠ + ٤٣ = ١٣٣°
إذاً الزاويتان غير متتامتان وغير متكاملتان.
٥) .JPG)
مجموع الزاويتان = ٦١ + ١١٩ = ١٨٠°
إذاً الزاويتان متكاملتان.
٦) .JPG)
مجموع الزاويتان = ٩٠ + ٩٠ = ١٨٠°
إذا الزاويتان متكاملتان.
٧) .JPG)
بما أن مجموع الزاويتان ١٨٠°
إذاً الزاويتان متكاملتان.
٨) .JPG)
بما أن مجموع الزاويتان ٩٠°
إذاً الزاويتان متتامتان.
٩) .JPG)
بما أن مجموع الزاويتان أكبر من ٩٠° وأقل من ١٨٠°
إذاً الزاويتان غير متكاملتان وغير متتامتان.
١٠) جبر: إذا كانت أ و ب متتامتين، وكان قب يساوي ٦٧° فما قأ؟
بما أن U أ و U ب متتامتان، ق U ب = ٦٧°
إذاً U أ + U ب = ٩٠°
U أ + ٦٧° = ٩٠°
U أ = ٢٣°
١١) جبر: أوجد قج إذا كانت ج و د متكاملتان، وكان قد يساوي ١١٥°.
بما أن U ج و U د متكاملتان، ق U د = ١١٥°
إذاً U ج + U د = ١٨٠°
U ج + ١١٥ = ١٨٠ اطرح ١١٥ من الطرفين.
U ج = ٦٥°
١٢) أدوات مدرسية: ما قياس الزاوية المجاورة في الشكل المجاور؟
بما أن الزاويتين تصنعان زاوية مستقيمة، مجموع الزاويتان = ١٨٠°
١١٦ + س = ١٨٠° اطرح ١١٦ من الطرفين.
س = ٦٤°
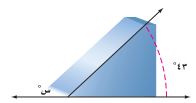
١٣) لوح التزلج: تشكل قاعدة التزلج في الشكل المجاور زاوية قياسها ٤٣° أوجد قياس الزاوية المجهولة.
الزاويتان متكاملتان أي مجموعهما ١٨٠°
٤٣ + س = ١٨٠ اطرح ٤٣ من الطرفين.
س = ١٣٧°
استعمل الشكل المجاور للإجابة عن الأسئلة ١٤ - ١٦.
١٤) سم زوجاً من الزوايا المتتامّة.
U ج ر ك و U ك ر ي.
١٥) سم زوجاً من الزوايا المتكاملة.
U ج ر د و U ج ر ي.
١٦) سم زوجاً من الزوايا المتقابلة بالرأس.
U ب ك أ وU ر ك ي.
هندسة: استعمل الشكل المجاور للإجابة عن الأسئلة ١٧ - ٢٠.
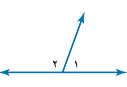
١٧) حدد ما إذا كان كل زوج من الزوايا ١ و ٢، ٢ و ٣، ١ و ٣ يمثل زاويتين متقابلتين بالرأس أو متجاورتين أو غير ذلك.
U ١ وU ٢ متجاورتين.
U ٢ وU ٣ متجاورتين.
U ٢ وU ٣ متقابلتين بالرأس.
١٨) اكتب معادلة تمثل مجموع ق١ و ق ٢ ومعادلة أخرى تمثل مجموع ق٢ و ق٣.
مجموع ق U ١ +ق U ٢ = ١٨٠° ١
مجموع ق U ٢+ U ٣ = ١٨٠° ٢
١٩) حل المعادلتين اللتين كتبتهما في السؤال ١٨ لحساب ق١، و ق٣ على الترتيب بدلالة ق٢. ما الذي تلاحظه؟
U ١ = ١٨٠ - U ٢ ٣
U ٣ = ١٨٠ - U ٢
ألاحظ أن المعادلتين متماثلتين.
٢٠) خمن: استعن بإجابتك في السؤال ١٩ لتخمين العلاقة بين الزوايا المتقابلة بالرأس.
استنتج أن الزوايا المتقابلة بالرأس متساوية.
أوجد قيمة س في كل من الأشكال الآتية:
٢١) .JPG)
بما أن الزاويتين متقابلتين بالرأس، إذا متساويتين،
س = ٤٠°
٢٢) .JPG)
بما أن الزاويتين متتامتين، مجموعهما = ٩٠°
س = ٩٠ - ٣٥ = ٥٥°
٢٣) .JPG)
بما أن الزاويتين متكاملتين، مجموعهما = ١٨٠°
س = ١٨٠ - ٢٠ = ١٦٠°
٢٤) اختيار من متعدد: مستعيناً بالشكل المجاور، أي الجمل الآتية صحيحة؟
أ) ١ و ٢ متكاملتان.
ب) ١ و ٢ متقابلتان بالرأس
جـ) ١ و ٢ متتامتان.
د) ١ و ٢ قائمتان.
الجملة الصحيحة أ) U ١ وU ٢ متكاملتان.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)

.JPG)
.JPG)