حلول الأسئلة
السؤال
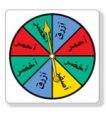
إذا أدير مؤشر القرص المجاور مرة واحدة فأوجد احتمال كل من الحوادث الآتية ثم اكتب إجابتك في صورة كسر اعتيادي:
الحل
شاهد حلول جميع الاسئلة
حل أسئلة تدرب وحل المسائل
إذا أدير مؤشر القرص المجاور مرة واحدة فأوجد احتمال كل من الحوادث الآتية ثم اكتب إجابتك في صورة كسر اعتيادي:
٨- ح (أزرق).
= عدد النواتج في الحادثة / العدد الكلي للنواتج الممكنة =
٩- ح (برتقالي).
=
١٠- ح (أحمر أو أصفر).
=
١١- ح (أحمر أو أصفر أو أخضر).
١٢- ح (ليس بنياً).
ح(بني) + ح (ليس بني) = ١
إذن احتمال عدم ظهور بني هو
١٣- ح (ليس أخضر).
ح(أخضر) + ح (ليس أخضر) = 1
سحبت بطاقة واحدة عشوائياً من بين ١٠ بطاقات مرقمة بالأرقام من ١ إلى ١٠ أوجد احتمال كل من الحوادث الآتية ثم اكتب إجابتك في صورة كسر اعتيادي:
١٤- ح (٨)
= عدد النواتج في الحادثة / العدد الكلي للنواتج الممكنة =
١٥- ح (٧ أو ٩)
=
١٦- ح (أقل من ٥)
=
١٧- ح (أكبر من ٣)
=
١٨- ح (فردي)
=
١٩- ح (زوجي)
=
٢٠- ح (ليس من مضاعفات ٤)
ح (مضاعفات ٤) + ح (ليس من مضاعفات ٤) = ١
إذن احتمال عدم ظهور عدد من مضاعفات ٤ هو
٢١- ح (ليس ٥ أو ٦ أو ٧ أو ٨)
ح (٥ أو ٦ أو ٧ أو ٨) + ح (ليس ٥ أو ٦ أو ٧ أو ٨) = ١
إذن احتمال عدم الظهور هو
تحليل جداول: استعمل الجدول المجاور الخاص بالرحلات الجوية في خمسة من المطارات للإجابة عن السؤالين ٢٢، ٢٣:
| الرحلات الجوية | |
| المطار |
النسبة المئوية للوصول الطائرات في موعدها |
| الأول | ٨٠ |
| الثاني | ٨٢ |
| الثالث | ٧٧ |
| الرابع | ٨٣ |
| الخامس | ٧٦ |
٢٢- إذا اختيرت إحدى الطائرات التي وصلت إلى المطار الأول عشوائياً فما احتمال ألا تكون قد وصلت في موعدها؟
ح (وصلت في موعدها) + ح (لم تصل في موعدها) = ١
٨٠٪ + ٢٠٪ = ١
إذن احتمال عدم وصولها في موعدها = ٢٠ ٪ = ٠.٢ =
٢٣- إذا اختيرت إحدى الطائرات التي وصلت إلى المطار الرابع عشوائياً فما احتمال ألا تكون قد وصلت في موعدها؟
احتمال أن تكون وصلت في موعدها هو = ٨٣٪ = ٠.٨٣ =
إذا التقطت خرزة واحدة من الوعاء المجاور دون النظر فيه فاكتب جملة تبين إمكانية وقوع كل من الحوادث الآتية وبرر إجابتك:
٢٤- الخرزة سوداء.
= ٠ يستحيل اختيار حبة حلوى سوداء.
٢٥- الخرزة بنفسجية.
= عدد النواتج في الحادثة/العدد الكلي للنواتج الممكنة.
=
فرصة اختيار حبة بنفسجية يساوي فرصة عدم اختيارها.
٢٦- الخرزة بنفسجية أو حمراء أو صفراء.
=
فرصة اختيار حبة بنفسجية أو حمراء أو صفراء كبيرة جداً.
٢٧- الخرزة خضراء.
= اختيار حبة خضراء أقل احتمالاً.
٢٨- مدرسة: يشكل طلاب المرحلة الابتدائية ٤٦٪ من طلاب مدارس البنين في المملكة العربية السعودية إذا اختير أحد المملكة لإجراء مقابلة معه فصف متممة حادثة اختيار طالب من المرحلة الابتدائية وأوجد احتمال المتممة اكتب إجابتك في صورة كسر اعتيادي وكسر عشري ونسبة مئوية.
ح (الحادثة) + ح (ليس حادثة) = ١
٤٦٪ + ٤٦٪ = ١
على صورة كسر عشري = ٠.٥٤
على صورة نسبة مئوية = ٥٤ ٪
على صورة كسر اعتيادي =
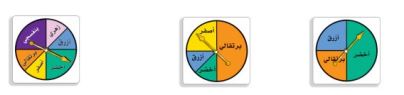
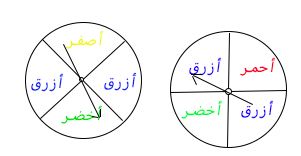
الهندسة: استعمل الأشكال الموضحة أدناه والمعلومات في الإجابة عن السؤالين ٢٩ - ٣٠:
يمكن حساب احتمال وقوف المؤسر عند أي جزء من القرص بأخذ قياس الزاوية التي يشكلها ذلك الجزء في الحسبان ففي الشكل الأول الزاوية التي يشكلها الجزء الأزرق تساوي ربع الزاوية المكونة من الدائرة الكاملة من الدائرة كاملة؛ لذا فإن ح (أزرق) = أو ٠.٢٥ أو ٢٥٪
٢٩- أوجد ح(أخضر) لكل شكل ثم اكتب الاحتمال في صورة كسر اعتيادي وكسر عشري ونسبة مئوية وبرر إجابتك.
ح (أخضر)١ = = ٠,٥ = ٥٠٪
الجزء الأخضر في الشكل الأول نصف الدائرة.
ح (أخضر)٢ = = ٠,١٢٥ = ١٢,٥ ٪
الجزء الأخضر في الشكل الأول نصف الدائرة.
ح (أخضر) ٣ = ٠,٢٥ = ٢٥٪
الجزء الأخضر في الشكل الثالث ربع الدائرة.
٣٠- أوجد ح (ليس برتقالياً) لكل شكل ثم اكتب الاحتمال في صورة كسر اعتيادي وكسر عشري ونسبة مئوية وبرر إجابتك.
ح (برتقال) + ح (ليس برتقالي) = ١ (شكل١).
١
إذن احتمال أن لا يكون برتقالي = = ٠,٧٥ = ٧٥٪
الجزء البرتقالي في الشكل الأول ربع الدائرة
ح (برتقال) + ح (ليس برتقالي) = ١ (شكل٢).
إذن احتمال أن لا يكون برتقالي = = ٠,٥٠ = ٥٠٪
الجزء البرتقالي في الشكل الثاني نصف الدائرة
ح(برتقال) + ح (ليس برتقالي) = ١ (شكل٣).
إذن احتمال أن لا يكون برتقالي = = ٠,٨٧٥ = ٨٧,٥ ٪
٣١- اكتشف الخطأ: حسب كل من سالم وأحمد احتمال ظهور العدد ٣ عند رمي مكعب الأرقام فأيهما كانت إجابته صحيحة؟ فسر إجابتك.
أحمد هو الصحيح لأنه اعتبر ٣ ناتجاً ممكناً واختاره من بين النواتج.
ح (٣) = عدد النواتج في الحادثة / العدد الكلي للنواتج الممكنة =
٣٢- تحد: إذا كان عدد الأجزاء في لعبة القرص ذي المؤشر أكثر من ثلاثة وكانت كلها متطابقة وكان احتمال وقوف مؤشر القرص على اللون الأزرق يساوي ٠,٥ فصمم شكلين ممكنين لهذه اللعبة وفسر لماذا يكون كل منهما مقبولاً.
التفسير أم كل من الجزئيين يساوي ٠,٥
٣٣- اكتب: شرحاً للعلاقة بين احتمال حادثة واحتمال متممتها ثم أعط مثالاً على ذلك.
احتمال الحادث = عدد النواتج في الحادثة / العدد الكلي للنواتج الممكنة.
ولكن احتمال متممتها = ح (الحدث)+ ح (عدم وجود الحدث) = ١
مثال: إذا كان احتمال سقوط المطر ٣٠ ٪ فاحتمال المتممة وهي سقوط المطر ٧٠٪
ومن المؤكد أن أحد هذين الأمرين سوف يتحقق.
٣٤- يحتوي وعاء على كرات ملونة بحسب الجدول أدناه إذا تم اختيار كرة دون النظر فيه فما احتمال أن تكون الكرة برتقالية؟
| اللون | عدد الكرات |
| أحمر | ٥ |
| برتقالي | ٣ |
| أصفر | ١ |
| أخضر | ٦ |
أ.
ب.
جـ.
د.
٣٥- في مزهرية مجموعة ٧ منها زرقاء و٦ خضراء و٣ صفراء و٨ حمراء وأراد تركي اختيار وردة دون النظر إلى الوردات فما احتمال ألا تكون الوردة خضراء؟
أ.
ب.
جـ.
د.

.JPG)
.JPG)

.JPG)