حلول الأسئلة
السؤال
أوجد مساحة متوازي أضلاع طول قاعدته سم، وارتفاعه سم.
الحل
مساحة متوازي الأضلاع = ق × ع
= ×
=
شاهد حلول جميع الاسئلة
حل أسئلة الاختبار التراكمي للفصل العاشر
اختر الإجابة الصحيحة:
١- الجدول أدناه يوضح مساحات مجموعة من المثلثات لها الارتفاع نفسه ولكنها تختلف في طول القاعدة:
| مساحات المثلثات | ||
|
الارتفاع (وحدات) |
طول القاعدة (وحدات) |
المساحة (وحدات مربعة) |
| ٤ | ٣ | ٦ |
| ٤ | ٤ | ٨ |
| ٤ | ٥ | ١٠ |
| ٤ | ٦ | ١٢ |
| ٤ | ن | ..... |
أي العبارات الآتية يمكن استعمالها لإيجاد مساحة مثلث ارتفاعه ٤ وحدات وطول قاعدته ن وحدة؟
أ.
ب.
جـ.
د. ٤ ن
٢- إذا كانت مساحة المثلث أدناه ٤٢,٢٥ سم٢ فما ارتفاعه؟
أ. ٦,٥ سم.
ب. ٢٦ سم.
جـ. ١٣سم.
د. ١١٩ سم.
٣- إذا كان ثمن أقلام ١٥ ريالاً فأي تناسب مما يأتي يمكن استعماله لإيجاد ثمن ١٩ قلماً من النوع نفسه؟
أ.
ب.
جـ.
د.
٤- حديقة دائرية الشكل قطرها ٨ م فأي مما يأتي يعبر عن العلاقة التقريبية بين قطر الحديقة (ق) ومحيطها (مح)؟
أ. ق ≈ مح
ب. ق ≈ مح
جـ. ق ≈ ٢ مح
د. ق≈ ٣ مح
٥- مثلث متطابق الضلعين زاويتا قاعدته متطابقتان وقياس زاوية رأسه ٤٠° فأي الطرق الآتية يمكن استعمالها لإيجاد قياس كل زاوية من زاويتي القاعدة؟
أ. اضرب ٤٠° في ٢ ثن أضف ١٨٠°
ب. اطرح ٤٠° إلى ١٨٠° ثم اقسم على ٢
جـ. أضف ٤٠° إلى ١٨٠° ثم اقسم على ١
د. اقسم ٥٠° إلى ٢ ثم اطرح من ١٨٠°
٦- منشور رباعي طوله ٦سم وعرضه ٥ سم وارتفاعه ٤ سم فما حجمه؟
أ. ١٥ سم٣
ب. ٦٠ سم٣
جـ. ٣٠ سم٣
د. ١٢٠ سم٣
٧- أوجد طول نصف قطر دائرة محيطها ٣٧,٦٨ سم بصورة تقريبية.
أ. ١٢ سم.
ب. ٦ سم.
جـ. ٥ سم.
د. ٣ سم.
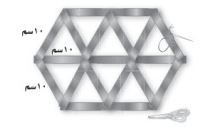
٨- استعملت ريم شريطاً من القماش لتزيين غلاف هديتها على هيئة مثلثات متطابقة الأضلاع كما في الشكل أدناه احسب طول الشريط الذي استخدمته في تغليف الهدية.
أ. ١٩٠ سم.
ب. ٣٠٠ سم.
جـ. ١٨٠ سم.
د. ٢٧٠ سم.
٩- أي الزوايا الآتية قياسها بين ٤٥°، ٩٠°؟
أجب عن السؤالين الآتيين:
١٠- أوجد قياس ٢ بالدرجات في المستطيل أ ب جـ د الموضح أدناه.
الزاوية أ قياسها = ٩٠°
إذن الزاوية ٢ = ٩٠° - ٢٧° = ٦٣°
١١- أوجد مساحة متوازي أضلاع طول قاعدته سم، وارتفاعه سم.
مساحة متوازي الأضلاع = ق × ع
= ×
=
١٢- اكتب النسبة المئوية ٨ ٪ في صورة كسر اعتيادي في أبسط صورة.
٨٪ =
أجب عن السؤال الآتي موضحاً خطوات الحل:
١٣- تحتفظ هيفاء بعقد ذهبي في علبة طولها ١٥ سم وعرضها ٩ سم وارتفاعها ٣ سم.
أ. أوجد مساحة السطح الكلية للعلبة وحجمها.
م = ٢ ل ض + ٢ ل ع + ٢ ض ع
= ٢(١٥) (٩) + ٢(١٥) (٣) + ٢(٩) (٣)
= ٣٠ × ٩ + ٣٠ × ٣ + ١٨ × ٣
= ٢٧٠ + ٩٠ + ٥٤
= ٤١٤ سم٢
ح = ل ض ع
= ١٥ × ٩ × ٣
= ٤٠٥ سم٣
ب. كم تصبح كل من مساحة السطح الكلية والحجم إذا أصبح كل بعد من أبعادها مثليه؟
إذا أصبح كل بعد من أبعاد العلبة مثليه.
م = ٢(١٥×٢) (٩ ×٢) + ٢(١٥ × ٢) (٣ ×٢) + ٢(٩ × ٢) (٣ × ٢)
= ١٠٨٠ + ٣٦٠ + ٢١٦
= ١٦٥٦ سم٢
ح = ١٥ × ٢ × ٩ × ٢ × ٣ × ٢ = ٣٢٤٠ سم٣
جـ. إذا أصبح أحد الأبعاد مثلي طوله الأصلي فما تأثير ذلك في كل من مساحة السطح الكلية والحجم؟ وهل يؤثر نوع البعد الذي يتم تغييره في النتيجة؟ فسر إجابتك.
إذا أصبح الارتفاع مثلي طوله الأصلي أي ٢ × ٣ = ٦ سم.
مساحة السطح الجديدة = (٢ × ١٥ × ٩) + (٢ × ١٥ × ٦) + (٢ × ٩ × ٦) = ٢٧٠ + ١٨٠ + ١٠٨ = ٥٥٨ سم٢
ومن ذلك نستنتج أن إذا أصبح أحد الأبعاد مثلي طوله الأصلي فإن مساحة السطح الكلية ستختلف بناء على البعد الذي أصبح مثلي طوله الأصلي.
الحجم الجديد = ١٥ × ٩ × ٦ = ٨١٠ سم٣
من ذلك نستنتج أن إذا أصبح أحد الأبعاد مثلي طوله الأصلي فإن الحجم الجديد يساوي مثلي الحجم الأصلي.


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)