حلول الأسئلة
السؤال
ستكتشف من خلال حل هذه المسألة المزيد حول طريقة كتابة المعادلات.
كيف يتغير عدد المكعبات في المجسم كلما زادت الطبقات؟
الحل
يضاف ٤ مكعبات إلى كل طبقة عن سابقتها.
شاهد حلول جميع الاسئلة
حل أسئلة تدرب وحل المسائل
أوجد مجموعة الحل لكل معادلة فيما يأتي إذا كانت (ص) تنتمي إلى مجموعة التعويض {١، ٣، ٥، ٧، ٩}، (ع) تنتمي إلى مجموعة التعويض {١٠، ١٢، ١٤، ١٦، ١٨}:
١١) ع + ١٠ = ٢٢
استبدل ع في المعادلة ع + ١٠ = ٢٢ بجميع قيم مجموعة التعويض.
| ع | ع + ١٠ = ٢٢ | صحيح أم خطأ |
| ١٠ | ١٠ + ١٠ = ٢٢ | خطأ |
| ١٢ | ١٢ + ١٠ = ٢٢ | صحيح |
| ١٤ | ١٤ + ١٠ = ٢٢ | خطأ |
| ١٦ | ١٦ + ١٠ = ٢٢ | خطأ |
| ١٨ | ١٨ + ١٠ = ٢٢ | خطأ |
بما أن المعادلة صحيحة عندما ع = ١٢، فإن حل المعادلة ع + ١٠ = ٢٢ هو ع = ١٢
وتكون مجموعة حل المعادلة: {١٢}.
١٢) ٥٢ = ٤ع
استبدل ع في المعادلة ٥٢ = ٤ع بجميع قيم مجموعة التعويض.
| ع | ٥٢ = ٤ ع | صحيح أم خطأ |
| ١٠ | ٥٢ = ٤ × ١٠ | خطأ |
| ١٢ | ٥٢ = ٤ × ١٤ | خطأ |
| ١٤ | ٥٢ = ٤ × ١٤ | خطأ |
| ١٦ | ٥٢ = ٤ × ١٦ | خطأ |
| ١٨ | ٥٢ = ٤ × ١٨ | خطأ |
بما أن المعادلة غير صحيحة عند جميع قيم التعويض.
ليس لها حل.
١٣) = ٣
استبدل ص في المعادلة = ٣ بجميع قيم مجموعة التعويض.
| ص | = ٣ | صحيح أم خطأ |
| ١ | = ٣ | خطأ |
| ٣ | = ٣ | خطأ |
| ٥ | = ٣ | صحيح |
| ٧ | = ٣ | خطأ |
| ٩ | = ٣ | خطأ |
بما أن المعادلة صحيحة عندما ص = ٥، فإن حل المعادلة = ٣ هو ص = ٥
وتكون مجموعة حل المعادلة: {٥}.
١٤) ١٧ = ٢٤ - ص
استبدل ص في المعادلة ١٧ = ٢٤ - ص بجميع قيم مجموعة التعويض.
| ص | ١٧ = ٢٤ - ص | صحيح أم خطأ |
| ١ | ١٧ = ٢٤ - ١ | خطأ |
| ٣ | ١٧ = ٢٤ - ٣ | خطأ |
| ٥ | ١٧ = ٢٤ - ٥ | خطأ |
| ٧ | ١٧ = ٢٤ - ٧ | صحيحة |
| ٩ | ١٧ = ٢٤ - ٩ | خطأ |
بما أن المعادلة صحيحة عندما ص = ٧، فإن حل المعادلة ١٧ = ٢٤ - ص هو ص = ٧
وتكون مجموعة حل المعادلة: {٧}.
١٥) ٢ع - ٥ = ٢٧
استبدل ع في المعادلة ٢ع - ٥ = ٢٧ بجميع قيم مجموعة التعويض.
| ع | ٢ع - ٥ = ٢٧ | صحيح أم خطأ |
| ١٠ | ٢ × ١٠ - ٥ = ٢٧ | خطأ |
| ١٢ | ٢ × ١٢ - ٥ = ٢٧ | خطأ |
| ١٤ | ٢ × ١٤ - ٥ = ٢٧ | خطأ |
| ١٦ | ٢ × ١٦ - ٥ = ٢٧ | صحيحة |
| ١٨ | ٢ × ١٨ - ٥ = ٢٧ | خطأ |
بما أن المعادلة صحيحة عندما ع = ١٦، فإن حل المعادلة ٢ع - ٥ = ٢٧ هو ع = ١٦
وتكون مجموعة حل المعادلة: {١٦}.
١٦) ٤(ص + ١) = ٤٠
استبدل ص في المعادلة ٤(ص + ١) = ٤٠ بجميع قيم مجموعة التعويض.
| ص | ١٧ = ٢٤ - ص | صحيح أم خطأ |
| ١ | ٤(١ + ١) = ٤٠ | خطأ |
| ٣ | ٤(٣ + ١) = ٤٠ | خطأ |
| ٥ | ٤(٥ + ١) = ٤٠ | خطأ |
| ٧ | ٤(٧ + ١) = ٤٠ | خطأ |
| ٩ | ٤(٩ + ١) = ٤٠ | صحيح |
بما أن المعادلة صحيحة عندما ص = ٩، فإن حل المعادلة ٤(ص + ١) = ٤٠ هو ص = ٩
وتكون مجموعة حل المعادلة: {٩}.
حل كل معادلة فيما يأتي:
١٧) أ = ٣٢ - ٩(٢)
أ = ٣٢ - ٩(٢) المعادلة الأصلية
أ = ٣٢ - ١٨ اضرب ٢ × ٩
أ = ١٤ اطرح ١٨ من ٣٢
القيمة الوحيدة لـ أ التي تجعل المعادلة صحيحة هي ١٤
لذا يكون لهذه المعادلة حل وحيد هو {١٤}.
١٨) و = ٥٦ ÷ (٢٢ + ٣)
و = ٥٦ ÷ (٢٢ + ٣) المعادلة الأصلية
و = ٥٦ ÷ (٤ + ٣) حساب القوى
و = ٥٦ ÷ ٧ اقسم ٥٦ ÷ ٧
و = ٨
القيمة الوحيدة لـ أ التي تجعل المعادلة صحيحة هي ٨
لذا يكون لهذه المعادلة حل وحيد هو {٨}.
١٩) = جـ
= جـ المعادلة الأصلية
= جـ اجمع ٢٧ + ٥
جـ = ٢ اقسم ٣٢ ÷ ١٦
القيمة الوحيدة لـ جـ التي تجعل المعادلة صحيحة هي ٢
لذا يكون لهذه المعادلة حل وحيد هو ٢.
٢٠) أ = + ٧
أ = + ٧ المعادلة الأصلية
أ = + ٧ اجمع ٢٧ + ٥
أ = + ٧ اقسم ٣٢ ÷ ١٦
أ = + ٧ اضرب ٤ × ١٣
أ = ٤ + ٧ = ١١ اقسم ٥٢ ÷ ١٣
القيمة الوحيدة لـ أ التي تجعل المعادلة صحيحة هي ١١
٢١) (٤ - ٢٢ + ٥) و = ٢٥
(٤ - ٢٢ + ٥) و = ٢٥المعادلة الأصلية
(٤ - ٤ + ٥) و = ٢٥ حساب القوى
٥و = ٢٥ اقسم ٥٦ ÷ ٧
و = ٥ اقسم طرفي المعادلة على ٥
القيمة الوحيدة لـ والتي تجعل المعادلة صحيحة هي ٥
لذا يكون لهذه المعادلة حل وحيد هو {٥}.
٢٢) ٧ + س -(٣ + ٣٢ ÷ ٨) = ٣
٧ + س -(٣ + ٣٢ ÷ ٨) = ٣ المعادلة الأصلية
٧ + س -(٣ + ٤) = ٣ حساب القوى
٧ + س - ٧ = ٣ اقسم ٥٦ ÷ ٧
س = ٣ اقسم طرفي المعادلة على ٥
القيمة الوحيدة لـ س التي تجعل المعادلة صحيحة هي ٣
لذا يكون لهذه المعادلة حل وحيد هو {٣}.
٢٣) ٢٣ - ٢ × ٣ + ي = (٣٣ - ٣ × ٨) (٢) + ي
٢٣ - ٢ × ٣ + ي = (٣٣ - ٣ × ٨) (٢) + ي
٩ - ٦ + ي = (٢٧ - ٢٤) (٢) + ي
٣ + ي = (٣) (٢) + ي
٣ + ي = ٦ + ي
عند التعويض بأي عدد حقيقي بدلاً من ي في المعادلة يكون دائماً الطرف الأيسر أكبر من الطرف الأيمن، لذا لا يمكن أن تكون المعادلة صحيحة.
وبالتالي فالمعادلة لا يوجد حل لها.
٢٤) ٦ك + (٣ × ١٠ - ٨) = (٢ × ٣) ك + ٢٢
٦ك + (٣ × ١٠ - ٨) = (٢ × ٣) ك + ٢٢
٦ك + (٣٠ - ٨) = (٦) ك + ٢٢
٦ك + ٢٢ = ٦ك + ٢٢
عند التعويض بأي عدد حقيقي بدلاً من ك في المعادلة يكون دائماً الطرف الأيسر يساوي الطرف الأيمن، لذا مجموعة حل المعادلة: مجموعة الأعداد الحقيقية.
٢٥) (٣ × ٥) ن + (٢١ - ١٢) = ١٥ن + ٢٣
(٣ × ٥) ن + (٢١ - ١٢) = ١٥ن + ٢٣
(١٥) ن + (٩) = ١٥ن + ٩
١٥ن + ٩ = ١٥ن + ٩
عند التعويض بأي عدد حقيقي بدلاً من ن المعادلة يكون دائماً الطرف الأيسر يساوي الطرف الأيمن، لذا مجموعة حل المعادلة: مجموعة الأعداد الحقيقية.
٢٦) ر - (-١) = ر + ( ÷ ٣)
ر - (-١) = ر + ( ÷ ٣)
ر - ( - ١) = ر + ( ÷ ٣)
٣ر - (١ - ١) = ر + (٢٤ ÷ ٣)
٣ر = ر + ٨
٢ر = ٨
ر = ٤
القيمة الوحيدة لـ ر التي تجعل المعادلة صحيحة هي ٤.
لذا يكون لهذه المعادلة حل وحيد هو ٤.
٢٧) مدرسة: تتسع قاعة الاجتماعات في مدرسة لـ ٤٥ شخصاً على الأكثر، فإذا أراد مدير المدرسة ورائد النشاط والمرشد الطلابي الاجتماع ببعض الطلبة، شريطة أن يحضر كل طالب ولي أمره فما أكثر عدد من الطلبة يمكن أن يحضر الاجتماع؟
بفرض س أكثر عدد من الطلبة يمكن أن يحضر الاجتماع.
٣ + (س × ٢) = ٤٥
٣ + ٢س = ٤٥
٢س = ٤٢
س = ٢١
أكثر عدد من الطلبة ممكن أن يحضروا الاجتماع هو ٢١ طالب.
٢٨) هندسة: ثماني محيطه ١٢٨ سم، أوجد طول ضلعه.
٨س = ١٢٨
س = ١٦
طول ضلع الثماني = ١٦ سم.
٢٩) لياقة: يتمرن رياضي كتلته ٩١ كجم ٤ ساعات يومياً ويحتاج إلى ٢٨٣٦ سعراً حرارياً للحصول على الطاقة الأساسية اللازمة له. كما يحتاج خلال التدريب إلى ٣٠٩١ سعراً حرارياً إضافياً، اكتب معادلة لإيجاد السعرات الحرارية الكلية ك اللازمة لهذا الراضي، ثم حلها.
ك = ٢٨٣٦ + ٣٠٩١
ك = ٥٩٢٧ سعر حراري.
السعرات الحرارية الكلية اللازمة لهذا الرياضي = ٥٩٢٧ سعر حراري.
كون جدولاً لقيم كل معادلة فيما يأتي إذا كانت مجموعة التعويض المعطاة {-٢، -١، ٠، ١، ٢}.
٣٠) ص = ٣س - ٢
| س | ٣س - ٢ | ص |
| -٢ | ٣(-٢) -٢ | - ٨ |
| -١ | ٣(-١) -٢ | -٥ |
| ٠ | ٣(٠) -٢ | -٢ |
| ١ | ٣(١) -٢ | ١ |
| ٢ | ٣(٢) -٢ | ٤ |
٣١) ٣,٢٥س + ٠,٧٥ = ص
| س | ٣,٢٥س + ٠,٧٥ | ص |
| -٢ | ٣,٢٥(-٢) + ٠,٧٥ | -٥,٧٥ |
| -١ | ٣,٢٥(-١) + ٠,٧٥ | -٢,٥٠ |
| ٠ | ٣,٢٥(٠) + ٠,٧٥ | ٠,٧٥ |
| ١ | ٣,٢٥(١) + ٠,٧٥ | ٤,٠٠ |
| ٢ | ٣,٢٥(٢) + ٠,٧٥ | ٧,٢٥ |
حل كل معادلة فيما يأتي باستعمال مجموعة التعويض المعطاة:
٣٢) ت - ١٣ = ٧؛ {١٠، ١٣، ١٧، ٢٠}
استبدل ت في المعادلة ت - ١٣ = ٧ بجميع قيم مجموعة التعويض.
| ت | ت - ١٣ = ٧ | صحيح أم خطأ |
| ١٠ | ١٠ - ١٣ = ٧ | خطأ |
| ١٣ | ١٣ - ١٣ = ٧ | خطأ |
| ١٧ | ١٧ - ١٣ = ٧ | خطأ |
| ٢٠ | ٢٠ - ١٣ = ٧ | صحيح |
بما أن المعادلة صحيحة عندما ت = ٢٠، فإن حل المعادلة ت - ١٣ = ٧ هو ت = ٢٠
ويكون حل المعادلة: ٢٠.
٣٣) ١٤(س + ٥) = ١٢٦؛ {٣، ٤، ٥، ٦، ٧}
استبدل س في المعادلة ١٤ (س + ٥) = ١٢٦ بجميع قيم مجموعة التعويض.
| س | ١٤ (س + ٥) = ١٢٦ | صحيح أم خطأ |
| ٣ | ١٤(٣ + ٥) = ١٢٦ | خطأ |
| ٤ | ١٤(٤ + ٥) = ١٢٦ | صحيح |
| ٥ | ١٤(٥ + ٥) = ١٢٦ | خطأ |
| ٦ | ١٤(٦ + ٥) = ١٢٦ | خطأ |
| ٧ | ١٤(٧ + ٥) = ١٢٦ | خطأ |
بما أن المعادلة صحيحة عندما س = ٤، فإن حل المعادلة ١٤ (س + ٥) = ١٢٦ هو س = ٤
ويكون حل المعادلة: ٤.
٣٤) ٢٢ = ؛ {٦٢، ٦٤، ٦٦، ٦٨، ٧٠}
استبدل ن في المعادلة ٢٢ = بجميع قيم مجموعة التعويض.
| ن | ٢٢ = | صحيح أو خطأ |
| ٦٢ | ٢٢ = | خطأ |
| ٦٤ | ٢٢ = | خطأ |
| ٦٦ | ٢٢ = | صحيح |
| ٦٨ | ٢٢ = | خطأ |
| ٧٠ | ٢٢ = | خطأ |
ويكون حل المعادلة: ٦٦.
حل كل معادلة فيما يأتي:
٣٥) = د
= د المعادلة الأصلية
= د اضرب ٣ × ٩
= د اجمع ١ + ٤
= د اضرب ٤ × ١٣
د = ٥ اقسم ٢٥ على ٥
القيمة الوحيدة لـ د التي تجعل المعادلة صحيحة هي ٥
لذا يكون لهذه المعادلة حل وحيد هو ٥.
٣٦) جـ = ١٥ ÷ ٣ × ٥ - ٢٤
جـ = ١٥ ÷ ٣ × ٥ - ٢٤ المعادلة الأصلية
جـ = ١٥ ÷ ٣ × ٥ - ١٦ حساب القوى
جـ = ٥ × ٥ - ١٦ اقسم ١٥ ÷ ٣
جـ = ٢٥ - ١٦ اضرب ٥ × ٥
جـ = ٩ اطرح ١٦ من ٢٥
القيمة الوحيدة لـ جـ التي تجعل المعادلة صحيحة هي ٩
لذا يكون لهذه المعادلة حل وحيد هو {٩}.
٣٧) جـ + (٢٣ - ٣) = ٢١
جـ + (٢٣ - ٣) = ٢١ المعادلة الأصلية
جـ + (٩ - ٣) = ٢١ حساب القوى
جـ + ٦ = ٢١ اطرح ٣ من ٩
جـ = ١٥ اطرح ٦ من ٢ الطرفين
القيمة الوحيدة لـ جـ التي تجعل المعادلة صحيحة هي ١٥
لذا يكون لهذه المعادلة حل وحيد هو {١٥}.
٣٨) (٣ - ٣ × ٩) + (٧ - ٢٢) ب = ٢٤ب
(٣ - ٣ × ٩) + (٧ - ٢٢) ب = ٢٤ب المعادلة الأصلية
(٢٧ - ٣ × ٩) + (٧ - ٤) ب = ٢٤ب حساب القوى
(٢٧ - ٢٧) + (٣) ب = ٢٤ب
٣ب = ٢٤ب
٣ب - ٣ب = ٢٤ب - ٣ب
٢١ب = ٠
ب = ٠
حدد إذا كان العدد المعطى بجانب كل معادلة فيما يأتي يمثل حلاً لها أم لا.
٣٩) س + ٦ = ١٥؛ ٩
س + ٦ = ١٥ المعادلة الأصلية
س = ٩ اطرح ٦ من الطرفين
نعم، ٩ حلاً للمعادلة.
٤٠) ١٢ + ص = ٢٦؛ ١٤
١٢ + ص = ٢٦ المعادلة الأصلية
ص = ١٤ اطرح ١٢ من الطرفين
نعم، ١٤ حلاً للمعادلة.
٤١) ٢ت - ١٠ = ٤؛ ٣
٢ت - ١٠ = ٤ المعادلة الأصلية
٢ت = ١٤ اجمع ١٠ على الطرفين
ت = ٧ اقسم الطرفين على ٢
لا، ٣ ليست حلاً للمعادلة.
٤٢) = ٢٠؛ ١٠
= ٢٠ المعادلة الأصلية
ك = ٢٠ اضرب طرفي المعادلة في ٢
لا، ١٠ ليست حلاً للمعادلة.
٤٣) = -٣؛ -١١
= -٣ المعادلة الأصلية
= -٣
= -٣
نعم، -١١ حلاً للمعادلة.
٤٤) -٤ = ١٢؛ ٤٨
-٤ = ١٢؛ ٤٨ المعادلة الأصلية.
جـ - ١٢ = ٣٦ اضرب طرفي المعادلة ٣
جـ = ٤٨ اجمع ١٢ على طرفي المعادلة
نعم، ٤٨ حلاً للمعادلة.
كون جدولاً لقيم كل معادلة فيما يأتي إذا كانت مجموعة التعويض للمتغير س هي: {-٢، -٠،١، ١، ٢}
٤٥) ص = ٣س + ٥
| س | ٣س + ٥ | ص |
| -٢ | ٣(-٢) + ٥ | -١ |
| -١ | ٣(-١) + ٥ | ٢ |
| ٠ | ٣(٠) + ٥ | ٥ |
| ١ | ٣(١) + ٥ | ٨ |
| ٢ | ٣(٢) + ٥ | ١١ |
٤٦) -٢س -٣ = ص
| س | -٢س -٣ | ص |
| -٢ | -٢(-٢) -٣ | ١ |
| -١ | -٢(-١) -٣ | ٠ |
| ٠ | -٢(٠) -٣ | -٣ |
| ١ | -٢(١) -٣ | -٥ |
| ٢ | -٢(٢) -٣ | -٧ |
٤٧) ص = س + ٢
| س | س +٢ | ص |
| -٢ | (-٢) + ٢ | ١ |
| -١ | (-١) + ٢ | ١,٥ |
| ٠ | (٠) + ٢ | ٢ |
| ١ | (١) + ٢ | ٢,٥ |
| ٢ | (٢) + ٢ | ٣ |
٤٨) هندسة: مستطيل يزيد طوله على عرضه ٢سم، ومثلث متطابق الضلعين طول قاعدته ١٢ سم، ويزيد طول كل من ضلعيه الآخرين ١ سم على عرض المستطيل.
أ) ارسم كلاً من المستطيل والمثلث، واكتب أبعادها.
ب) اكتب عبارتين لإيجاد محيط كل من المستطيل والمثلث.
محيط المثلث = مجموع أطوال أضلاعه الثلاث
= ٢(س + ١) + ١٢
= ٢س + ١٤
محيط المستطيل = ٢ (الطول + العرض)
= ٢(س + س + ٢)
= ٢(٢س + ٢)
= ٤س + ٤
جـ) أوجد عرض المستطيل إذا كان له محيط المثلث نفسه.
محيط المثلث = محيط المستطيل
٢س + ١٤ = ٤س + ٤
٢س = ١٠س
س = ٥ سم
عرض المستطيل = ٥ سم
٤٩) إنشاءات: يحتاج بناء كل طابق في إحدى البنايات إلى ١٠ أطنان من الحديد.
أ) عرف متغيراً، واكتب معادلة لإيجاد كمية الحديد الضرورية لبناء ١٥ طابقاً.
افترض أن س كمية الحديد اللازمة لبناء ١٥ طابق.
س = ١٠ × ١٥
ب) كم طناً من الحديد يحتاج إليه البناء؟
س = ١٠ × ١٥
س = ١٥٠
إذن يحتاج بناء ١٥ طابق إلى ١٥٠ طن حديد.
٥٠) تمثيلات متعددة: ستكتشف من خلال حل هذه المسألة المزيد حول طريقة كتابة المعادلات.
أ) حسياً: استعمل المكعبات السنتمترية لبناء مجسم يشبه المجسم المجاور.
ب) جدولياً: انقل الجدول المبين أدناه إلى دفترك، وأكمله بتسجيل عدد طبقات المجسم والمكعبات المستعملة في ذلك.
| عدد الطبقات | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ |
| عدد المكعبات | ٤ | ٨ | ١٢ | ١٦ | ٢٠ | ٢٤ | ٢٨ |
جـ) تحليلياً: كيف يتغير عدد المكعبات في المجسم كلما زادت الطبقات؟
يضاف ٤ مكعبات إلى كل طبقة عن سابقتها.
د) جبرياً: اكتب قاعدة لإيجاد عدد المكعبات بدلالة عدد طبقات المجسم.
عدد المكعبات = ٤ط؛ ط عدد طبقات المجسم.
٥١) مقارنة: قارن بين المعادلة والعبارة الجبرية.
- العبارة الجبرية: تتكون من طرف واحد مثل ٤ص + ١١ ولا يوجد إشارة المساواة (=)
- المعادلة: بينهما إشارة المساواة (=) مثل ٥س + ١١ = ٢٤
٥٢) مسألة مفتوحة: اكتب معادلة تمثل متطابقة.
٣(ب + ١) - ٥ = ٣ب - ٢
٥٣) اكتشف الخطأ: حل عصام وعدنان المعادلة: س = ٤(٣ -٢) + ٦ ÷ ٨ كما هو مبين أدناه، أيهما على صواب؟ وضح إجابتك.
عصام؛ لأنه استعمل ترتيب العمليات، بينما عدنان لم يستعملها حيث جمع قبل أن يقسم.
٥٤) تحد: أوجد جميع حلول المعادلة: س + ٥ = ٣٠.
س + ٥ = ٣٠ المعادلة الأصلية.
س٢ = ٢٥ اطرح ٥ من طرفي المعادلة
س = الجذر التربيعي للطرفين
س = ٥، س = -٥
٥٥) اكتب: فسر كيف تحدد أن معادلة ما ليس لها حل حقيقي، وأن حل معادلة أخرى هو مجموعة الأعداد الحقيقية.
تحتوي المعادلات التي ليس لها حلول حقيقية على المتغيرات نفسها ومعاملاتها في طرفي المعادلة، مع اختلاف في عدد أو عملية ما، أما المعادلات التي لها المتغيرات والأعداد والعمليات نفسها في طرفيها فيكون حلها هو مجموعة الأعداد الحقيقية.
٥٦) اختيار من متعدد: يتوقع أن يحضر الحفل المدرسي ٦٥٪ من الطلاب، فإذا كان عدد الطلاب ٣٠٠ طالب، فكم طالباً يتوقع حضورهم؟
أ) ٥٠ طالباً.
ب) ٦٥ طالباً.
جـ) ١٠٥ طلاب.
د) ١٩٥ طالباً.
× ٣٠٠ = ١٩٥
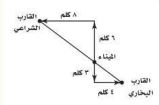
٥٧) هندسة: تحرك قارب بخاري وآخر شراعي من الميناء نفسه، ويبين الشكل أدناه حركتيهما، فما المسافة بين القاربين؟
أ) ١٢ كلم.
ب) ١٥ كلم.
جـ) ١٨ كلم.
د) ٢٤ كلم.
- المسافة بين الميناء والقارب البخاري = = ٥ كلم.
- المسافة بين الميناء والقارب البخاري = = ١٠ كلم.
- المسافة بين القاربين = ٥ + ١٠ = ١٥ كلم.
الإجابة ب) ١٥ كلم.

.JPG)
.JPG)
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)