حل أسئلة تدرب وحل المسائل
أوجد مساحة كل متوازي أضلاع فيما يأتي:
٦- .JPG)
م = ق ع مساحة متوازي الأضلاع.
= ٤ × ٤ ضع ٤ بدلاً من ق، و٤ بدلاً من ع.
= ١٦ وحدة٢
٧- 
م = ق ع.
= ٦ × ٤
= ٢٤ وحدة٢
٨- 
م = ق ع مساحة متوازي الأضلاع.
= ٨ × ٩
= ٧٢ سم٢
٩- 
م = ق ع مساحة متوازي الأضلاع.
= ١٢ × ٤
= ٤٨ م٢
١٠- 
م = ق ع مساحة متوازي الأضلاع.
= ١٢ × ١٥
= ١٨٠ كلم
١١- 
م = ق ع.
= ٣٧ × ٢٢
= ٨١٤ ملم٢
١٢- أوجد مساحة متوازي أضلاع طول قاعدته ٢٤ سم، وارتفاعه سم.
م = ق ع مساحة متوازي الأضلاع.
= ٢٤ ×
= ٥٤ سم٢
١٣- أوجد مساحة متوازي أضلاع طول قاعدته ٦,٧٥ سم وارتفاعه ٤,٨ سم.
م = ق ع مساحة متوازي الأضلاع.
= ٦,٧٥ × ٤,٨
= ٣٢,٤ م٢
١٤- موقف سيارة: أوجد مساحة موقف السيارة الموضح أدناه.
م = ق ع مساحة موقف سيارة.
= ٢,٤ × ٥,٤
= ١٢,٩٦ م٢
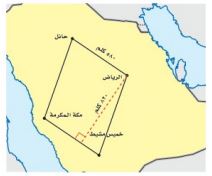
١٥- خرائط: أوجد مساحة المنطقة الموضحة في الخريطة أدناه.
م = ق ع.
= ٥٨٠ × ٨٢٠
= ٤٧٥٦٠٠ كلم٢
أوجد مساحة الجزء المظلل في كل شكل من الأشكال الآتية:
١٦- 
م١ = الطول × العرض.
= ٢٥ × ١١
= ٢٧٥ م٢
م٢ = ق ع
= ١٢ × ٤
= ٤٨ م٢
مساحة الجزء المظلل = م١ - م٢ = ٢٧٥ - ٤٨ = ٢٢٧ م٢
= ٢٧٥ - ٤٨ = ٢٢٧ م٢
١٧- 
م١ = طول الضلع × نفسه.
= ٦ × ٦
= ٣٦ سم٢
م٢ = ق ع
= ١٥ × ٨
= ١٢٠ سم٢
مساحة الجزء المظلل = م٢ - م١
= ١٢٠ - ٣٦ = ٨٤ سم٢
١٨- تخطيط: أرض على شكل متوازي أضلاع مساحتها ١٨٠٠م٢ ، إذا كان طول قاعدة متوازي الأضلاع ٧٥م فهل يمكن أن يكون ارتفاعه ٢١ م؟ فسر إجابتك.
لا تفسير الإجابة: م = ١٨٠٠ م
ق = ٧٥ م
ع =
=
=٢٤ م
١٩- تحليل جداول: الجدول المجاور يوضح ثلاثة تصاميم معمارية لثلاث حدائق مختلفة كل منها على شكل متوازي أضلاع أوجد البعد المجهول في كل منها.
| الحديقة | القاعدة (م) | الارتفاع (م) | المساحة (م٢) |
| ١ | ١٤٧ | ||
| ٢ | |||
| ٣ |
ارتفاع الحديقة ١ = المساحة ÷ القاعدة.
= ١٤٧ ÷ = ٩,٣٣٣ م
قاعدة الحديقة ٢ = المساحة ÷ الارتفاع.
= = ١٢,٥ م
ارتقاع الحديقة ٣ = المساحة ÷ القاعدة.
= ١٤,٧٥ م
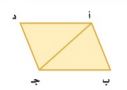
٢٠- تبرير: إذا كانت مساحة متوازي الأضلاع أ ب جـ د في الشكل المجاور تساوي ٣٥سم٢ ، فأوجد مساحة المثلث أ ب جـ.
مساحة المثلث = نصف مساحة متوازي الأضلاع.
= ٠,٥ × ٣٥ = ١٧,٥ سم٢
٢١- مسألة مفتوحة: ارسم في ورقة مربعات ثلاث متوازيات أضلاع مختلفة مساحة كل واحد منها ٢٤ وحدة مربعة وارتفاعه ٤ وحدات ثم بين أوجه الشبه وأوجه الاختلاف بينها.
- أوجه الشبه: كل متوازيات الأضلاع لها نفس قياس القاعدة والارتفاع والمساحة.
- أوجه الاختلاف: والاختلاف في الميل.
٢٢- تحد: إذا كانت س = ٥، ص < س فأي الشكلين مساحته أكبر؟ فسر إجابتك.
مساحة المستطيل أكبر.
تفسير الإجابة: مساحة المستطيل = ٥ × ص = ٥ ص وحدة٢
مساحة متوازي الأضلاع = س × ع
وحيث أن ص في متوازي الأضلاع يعتبر وتر المثلث الذي يحتوي ص والارتفاع، إذاً ع < ص
مساحة المستطيل > مساحة متوازي الأضلاع.
٢٣- اكتب: تفسير للعلاقة مساحة متوازي الأضلاع وصيغة مساحة المستطيل.
مساحة متوازي الأضلاع = ق × ع.
مساحة المستطيل = ل × ض.
المستطيل كل زواياه قائمة لذا يعتبر العرض (ض) ارتفاعاً للمستطيل.
٢٤- صمم سلمان شعار المحل تجاري من الورق المقوى على شكل متوازي أضلاع مساحته ١٨٧٢ سم٢ ، وطول قاعدته ٥٢ سم فأوجد ارتفاع الشعار.
أ. ٨٨٤ سم.
ب. ١٧٦ سم.
جـ. ٤٢ سم.
د. ٣٦ سم.
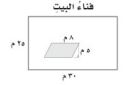
٢٥- لدى عائلة حديقة مزروعة بالورد على شكل متوازي أضلاع في فناء البيت الذي على شكل مستطيل كما في الشكل أدناه إذا زرعت أعشاب في باقي فناء البيت فما مساحة المنطقة المزروعة أعشاباً؟
أ. ٣٥٥ م٢
ب. ٣٣٥ م٢
جـ. ٧١٠ م٢
د. ٧٩٠ م٢
حلول أسئلة الصف السادس الابتدائي
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى


.JPG)
.JPG)

.JPG)
.JPG)
.JPG)
النقاشات