الدرس 4: خطة حل المسألة
١- اشرح كيف ساعد "أنشاء النموذج" طارقاً على حل المسألة.
ساعد طارق على فهم المسألة ومعرفة هل المائة مقعد يكفي لترتيب ٧ صفوف أم لا قبل القيام بترتيبها.
٢- اكتب مسألة يمكن حلها باستعمال "إنشاء نموذج" ثم اكتب خطوات الحل.
مذاكرة: يريد طارق أن يعمل جدولاً للمذاكرة يومياً فكتب ساعتين للعلوم ساعتين للدراسات و٣ ساعات للرياضيات و٥ ساعات اللغة العربية و٤ ساعات اللغة الإنجليزية استعمل خطة إنشاء نموذج لمعرفة هل يكفي اليوم الواحد لمذاكرة جميع هذه المواد؟
خطوات الحل:
أفهم: تعرف على أن اليوم ٢٤ ساعة والمطلوب معرفة هل اليوم يكفي لمذاكرة المواد أن لا.
خطط: أنشئ نموذجاً لمعرفة هل اليوم كافي أم لا.
حل: مجموع الساعات لمذاكرة المواد كلها.
= عدد ساعات العلوم + عدد ساعات الدراسات + عدد ساعات الرياضيات + عدد ساعات اللغة العربية + عدد ساعات الإنجليزية.
= ٢ + ٢ + ٣ + ٥ + ٤ = ١٦ ساعة.
إذن يكفي اليوم لمذاكرة المواد كلها.
تحقق: اليوم ٢٤ ساعة > ١٦ ساعة لذلك يكفي اليوم لمذاكرة المواد كلها.
استعمل خطة "إنشاء نموذج" لحل المسائل ٣ - ٥:
٣- هندسة: أوجد جميع الإمكانات لطول كل من القاعدة والارتفاع لمتوازي أضلاع مساحته ٢٤ سم٢ على أن تكون أعداداً صحيحة.
أفهم: مساحة متوازي الأضلاع = ٢٤ سم٢ أوجد جميع الإمكانات لطول القاعدة والارتفاع بحيث تكون أعداداً صحيحة.
خطط: أنشئ نموذجاً لمعرفة جميع الإمكانات لأطوال القاعدة والارتفاع.
حل: م = ق ع مساحة متوازي الأضلاع.
= ٢٤ سم٢
٢٤ = ٢ × ١٢
= ٤ × ٦
= ١ × ٢٤
= ٣ × ٨
إذن جميع إمكانات طول القاعدة هي ٢ - ٤ - ١ - ٣
فتكون جميع إمكانات طول الارتفاع هي ١٢ - ٦ - ٢٤ - ٨
ويمكن أن تكون جميع إمكانات طول القاعدة هي ١٢ - ٦ - ٢٤ - ٨
فتكون جميع إمكانات طول الارتفاع هي ٢ - ٤ - ١ - ٣
تحقق: عند التعويض بأطوال القاعدة والارتفاع في قانون مساحة متوازي الأضلاع نجد الإجابة هي ٢٤ سم٢ لجميع الاحتمالات.
إذن الإجابة صحيحة.
٤- تصميم: يريد مصمم ترتيب ١٢ طوبة زجاجية مربعة الشكل لتكوين مستطيل بأقل محيط ممكن فكم طوبة سيضع في كل صف؟
أفهم: تكوين مستطيل بأقل محيط ممكن من ١٢ طوبة زجاجية.
خطط: أنشئ نموذجاً لمعرفة كم طوبة في كل صف.
حل: يوضع في كل صف ٤ طوبات زجاجية فيكون ٣ صفوف أو يوضع في كل صف ٤ طوبات زجاجية فيكون ٤ صفوف عدد الصفوف = ٣
كل صف = ٤
تحقق: عدد الطوبات جميعها = ٣ × ٤ = ١٢ طوبة زجاجية.
إذن الإجابة صحيحة وعدد الطوبات الزجاجية.
٥- ورق: أخذ ماجد ورقة من دفتر الملاحظات وطواها نصفين ثم وضع القطعتين بعضهما فوق بعض وطواهما مرة ثانية فحصل على ٤ قطع إذا استمر على هذا النمط فما عدد القطع الورقية بعد الطي في المرة السادسة؟
أفهم: بعد طوي الورق مرتين حصل ماجد على أربع قطع فما عدد القطع الورقية بعد الطي السادس؟
خطط: أنشئ نموذجاً لمعرفة عدد القطع الورقية بعد الطي السادس.
حل: بعد الطي الثالث يحصل على ٨ قطع.
بعد الطي الرابع يحصل على ١٦ قطعة.
بعد الطي الخامس يحصل عل ٣٢ قطعة.
بعد الطي السادس يحصل على ٦٤ قطعة.
تحقق: في كل مرة يطوي فيها الورق يكون عدد القطع ضعف المرة السابقة لذلك عند مضاعفة عدد القطع في كل مرة نحصل على ٦٤ قطعة بعد الطي السادس.
إذن الإجابة صحيحة.
استعمل الخطة المناسبة مما يأتي لحل المسائل ٦ - ١٣:
٦- رياضة: من خلال مسح إحصائي شمل ٥٠ طالباً تبين أن ٢٢ طالباً منهم يفضلون لعبة كرة القدم و١٨ طالباً يفضلون كرة السلة و٦ طلاب يفضلون اللعبتين معاً ما عدد الطلاب الذين لا يفضلون أياً من اللعبتين؟
أفهم: العدد الكلي للطلاب = ٥٠ طالب.
عدد الذين يفضلون كرة القدم = ٢٢ طالب.
عدد الذين يفضلون كرة السلة = ١٨ طالب.
عدد الذين يفضلون اللعبتين = ٦ طلاب.
فما عدد الطلاب الذين لا يفضلون أياً من اللعبتين؟
خطط: أنشئ نموذجاً لمعرفة عدد الطلاب الذين لا يفضلون أياً من اللعبتين.
حل: عدد الطلاب الكلي = ٥٠ طالب، ٦ يفضلون اللعبتين معاً.
عدد الطلاب الذين يفضلون الألعاب = ٢٢ + ١٨ - ٦ = ٣٤ طالب.
إذن عدد الطلاب الذين لا يفضلون أياً من اللعبتين = ٥٠ - ٣٤ = ١٦ طلاب.
تحقق: عدد الطلاب الذين يفضلون الألعاب < عدد الطلاب الكلي ب ١٦ طلاب لذا فإنه يوجد ١٦ طلاب لا يفضلون أياً من اللعبتين.
إذن الإجابة صحيحة.
٧- أنماط: أكمل النمط الآتي لإيجاد الحد الرابع: (٢٥ - ٤٠ - ٥٥).
٢٥ - ٤٠ - ٥٥ في كل مرة نزود ١٥ عن المرة السابقة.
أفهم: إكمال النمط لإيجاد الحد الرابع.
خطط: ابحث عن نمط وهو إضافة ١٥ لكل حد.
حل: ٢٥ + ١٥ ٤٠ = ٤٠ + ١٥ = ٥٥ ٥٥ + ١٥ = ٧٠ إذن الحد الرابع هو ٧٠
تحقق: عند جمع ١٥ على الحد الأول نجد أن الحد الثاني هو ٤٠ وعند جمع ١٥ على ٤٠ نجد أن الحد الثالث هو ٥٥ وعند جمع ١٥ على ٥٥ نجد أن الحد الرابع هو ٧٠ إذن الإجابة صحيحة.
٨- ثقوب: طوى سهيل ورقة من دفتر الملاحظات من نصفها مرتين ثم عمل ثقباً عبر جميع الطبقات فإذا أعاد الورقة إلى وضعها الأصلي قبل الطي فما عدد الثقوب الموجودة فيها؟
أفهم: طوى سهيل الورقة مرتين ثم عمل ثقباً يمر بجميع الطبقات فما عدد الثقوب عند فرد الورقة؟
خطط: أنشئ نموذجاً لمعرفة عدد الثقوب عند فرد الورقة؟
حل: عدد الثقوب = ٤ ثقوب.
تحقق: عند طوي الورقة مرتين فتصبح ٤ طبقات لذا فعند عمل ثقب يمر بجميع الطبقات وفرد الورقة مرة أخرى يصبح عدد الثقوب = ٤ ثقوب.
إذن الإجابة صحيحة.
٩- هندسة: إذا كان قياس كل من القاعدة والارتفاع في كل مثلث من المثلثات أدناه يساوي نصف قياسها في المثلث السابق له فما مساحة المثلث الرابع؟
أفهم: قياس القاعدة للمثلث الأول = ٢٤ سم، وقياس الارتفاع له = ١٦ سم.
وقياس قاعدة وارتفاع المثلث التالي يساوي نصف قياس القاعدة والارتفاع للمثلث السابق له فأوجد مساحة المثلث الرابع.
خطط: أنشئ نموذجاً لمعرفة مساحة المثلث الرابع.
حل: قاعدة المثلث الثاني = ٠,٥ × ٢٤ = ١٢
ارتفاعه = ٠,٥ × ١٦ = ٨ سم.
قاعدة المثلث الثالث = ٠,٥ × ١٢ = ٦ سم.
ارتفاعه = ٠,٥ × ٨ = ٤ سم.
قاعدة المثلث الرابع = ٠,٥ × ٦ = ٣ سم.
ارتفاعه = ٠,٥ × ٤ = ٢ سم.
إذن مساحة المثلث الرابع = ق ع = (٣) (٢) = ٣ سم٢
تحقق: مساحة المثلث الثالث = ق ع
= (٦) (٤) = ١٢ سم٢
نجد أن مساحة المثلث الرابع تساوي ربع مساحة المثلث الثالث إذن قياس القاعدة والارتفاع للمثلث الرابع تساوي نصف قياسها للمثلث الثالث إذن الإجابة صحيحة.
طريقة أخرى بالبحث عن نمط:
حيث أن مساحة المثلث الثاني نصف مساحة الأول ومساحة المثلث الثالث نصف مساحة المثلث الثاني إذا فيكون النمط بالقسمة على ٢
١٠- حدائق: الجدول أدناه يبين أسعار تذاكر الدخول لحديقة الحيوانات في الرياض كم ريالاً ستدفع أسرة مكونة من أب وأم وأطفالها الثلاثة لدخول الحديقة؟
| الشخص | الكبار | الصغار |
| سعر التذكرة (ريال) | ١٠ | ٥ |
أفهم: سعر تذكرة دخول الكبار = ١٠ ريالات وسعر التذكرة للصغار = ٥
فكم ريالاً ستدفع أسرة مكونة من أب وأم وأطفالها الثلاثة؟
خطط: أنشئ نموذجاً لمعرفة عدد الريالات التي ستدفعها الأسرة.
حل: سعر التذكرة للأب والأم = ١٠ × ٢ = ٢٠ ريالاً.
سعر التذكرة للأطفال الثلاثة = ٥ × ٣ = ١٥ ريالاً.
إذن عدد الريالات الت ستدفعها الأسرة = ٢٠ + ١٥ = ٣٥ ريالاً.
تحقق: عدد الريالات التي ستدفعها الأسرة = ٣٥ ريالاً.
٣٥ = ١٠ + ١٠ + ٥ + ٥ + ٥
إذن فهي عبارة عن تذكرتين للكبار أي الأب والأم و٣ تذاكر للصغار أي الأطفال إذن الإجابة صحيحة.
١١- أقساط: اشترى خالد ثلاجة ثمنها ٣٠٠٠ ريال واتفق مع البائع على تقسيط المبلغ على أقساط شهرية مدة سنة أوجد مقدار القسط الشهري.
أفهم: سعر الثلاجة = ٣٠٠٠ ريالاً والتقسيط لمدة سنة أوجد مقدار القسط الشهري.
خطط: أنشئ نموذجاً لمعرفة مقدار القسط الشهري.
حل: السنة = ١٢ شهراً إذن مقدار القسط الشهري = = ٢٥٠ ريالاً.
تحقق: يدفع خالد ٢٥٠ ريالاً كل شهر لمدة سنة (١٢شهراً).
إذن عدد الريالات التي يدفعها في السنة = ٢٥٠ × ١٢ = ٣٠٠٠ ريالاً.
إذن الإجابة صحيحة.
١٢- دوائر: دائرتان قطر الأولى منهما ثلاثة أمثال قطر الثانية أوجد النسبة بين محيطيهما.
أفهم: قطر الدائرة الأولى ثلاث أمثال قطر الدائرة الثانية أوجد النسبة بين محيطيهما.
خطط: أنشئ نموذجاً لمعرفة النسبة بين محيط الدائرتين.
حل: محيط الدائرة الأولى = ط (٣ق).
محيط الدائرة الثانية = ط (ق).
إذن النسبة بين محيطيهما = =
إذن النسبة بين محيط الدائرة الأولى إلى محيط الدائرة الثانية = ١:٣
تحقق: محيط الدائرة الأولى ÷ محيط الدائرة الثانية = ١:٣
فإذا كان محيط الدائرة الثانية = ط(ق)
إذن محيط الدائرة الأولى = ٣
إذن الإجابة صحيحة.
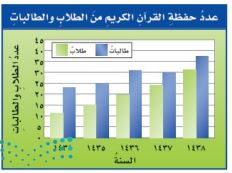
١٣- حفظ القرآن الكريم: معتمداً على التمثيل البياني أدناه الذي يبين أعداد الطلاب والطالبات الذين حفظوا القرآن الكريم في جمعية لتحفيظ القرآن كم يزيد عدد الحافظين عام ١٤٣٧ هـ على عددهم عام ١٤٣٥ هـ؟
أفهم: عدد الطلاب عام ١٤٣٠ هـ = ٣٠ طالب.
عددهم عام ١٤٢٨ هـ = ٢٥ طالب.
كم يزيد عدد الطلاب عام ١٤٣٠ هـ على عددهم عام ١٤٢٨ هـ؟
خطط: أنشئ نموذجاً لمعرفة مقدار زيادة الطلاب في عام ١٤٣٠ هـ عن عام ١٤٢٨ هـ
حل: مقدار زيادة الطلاب في عام ١٤٣٠ هـ عن عام ١٤٢٨ هـ
= ٣٠ - ٢٥ = ٥ طلاب.
تحقق: عدد الطلاب عام ١٤٢٨ هـ = ٢٥ طالب ويزيدون عن ذلك في عام ١٤٣٠ هـ بمقدار ٥ طلاب.
إذن عدد الطلاب في عام ١٤٣٠ هـ = ٢٥ + ٥ = ٣٠ طالب.
إذن الإجابة صحيحة.
حلول أسئلة الصف السادس الابتدائي
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى



.JPG)
.JPG)
.JPG)
.JPG)
النقاشات