تدرب وحل المسائل
حدد ما إذا كانت المعطيات في كل مما يأتي كافية ليكون الشكل الرباعي متوازي أضلاع أم لا. ثم برر إجابتك.
9)
الحل: نعم لأن كل ضلعين متقابلين متطابقين.
10)
الحل: نعم لأن كل ضلعين متقابلين متوازيين ومتطابقين.
11)
الحل: لا، لأنه لا يحقق أي واحد من اختبارات متوازي الأضلاع.
12)
الحل: لا؛ لأنه لا يحقق أي واحد من اختبارات متوازي الأضلاع.
13)
الحل: نعم لأن قطريه ينصف كل منهما الآخر.
14)
الحل: لا، لأنه لا يحقق أي واحد من اختبارات متوازي الأضلاع.
15) برهان: إذا كان WXYZ متوازي أضلاع حيث نقطة منتصف فاكتب برهاناً حراً لإثبات أن متطابق الضلعين.
الحل:
- المعطيات: wxyz متوازي أضلاع فيه نقطة منتصف
- المطلوب: متطابق الضلعين.
- البرهان: بما ان WXYZ متوازي أضلاع فإن وبما أن M نقطة منتصف فإن ومعطى أن لذلك وحسب SAS فإن ولأن العناصر المتناظرة في مثلثين متطابقين متطابقة فإن إذن ZMY مثلث متطابق الضلعين بحسب تعريف المثلث متطابق الضلعين.
16) رافعات: تستعمل رافعات متوازيات الأضلاع لرفع المركبات الثقيلة عند صيانتها ففي الشكل أدناه: ABEF, BCDE متوازيا أضلاع اكتب برهاناً ذا عمودين لإثبات أن ACDF متوازي أضلاع أيضاً.
الحل:
- المعطيات: ABFE متوازي أضلاع؛ BCDE متوازي أضلاع.
- المطلوب: ACDF متوازي أضلاع.
- البرهان: العبارات (المبررات):
1) ABEF متوازي أضلاع؛ BCDE متوازي أضلاع (معطيات).
2) (تعريف متوازي الأضلاع).
3)
4)ACDF متوازي أضلاع (إذا كان في كل شكل رباعي ضلعان متطابقان ومتوازيان فإنه متوازي أضلاع).
جبر: أوجد قيمتي x,y في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع.
17)
الحل:
18)
الحل:
19)
الحل:
20)
الحل:
21)
الحل:
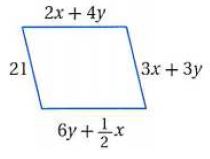
22)
الحل:
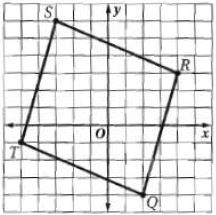
هندسة إحداثية: مثل في المستوى الإحداثي الشكل الرباعي المعطاة إحداثيات رؤوسه فيما يأتي وحدد ما إذا كان متوازي أضلاع أم لا ثم برر إجابتك باستعمال الطريقة المحددة في السؤال.
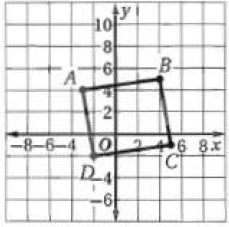
23) صيغة الميل.
الحل:
نعم؛ ميل يساوي ميل ويساوي لذلك
حيث أن الميل
وبما أن مبل يساوي ميل ويساوي 6-
فإن ولأن كل ضلعين متقابلين متوازيان فإن ABCD متوازي أضلاع.
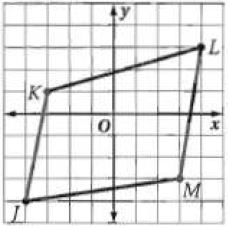
24) صيغة المسافة بين نقطتين.
الحل:
لا؛ يجب أن يكون ضلعين متقابلين متطابقين.
والمسافة بين K وL تساوي . والمسافة بين L وM تساوي .
والمسافة بين M وL تساوي . والمسافة بين J وK تساوي
حيث أن المسافة بين أي نقطتين
وبما أن كل ضلعين متقابلين ليسا متطابقين فإن JKLM ليس متوازي أضلاع.
25) صيغة الميل.
الحل:
وبما أن ميل -- لا يساوي ميل -- , وميل -- لا يساوي ميل -- فإن VWXY ليس متوازي أضلاع.
26) صيغتا الميل والمسافة بين نقطتين.
الحل:
يجب أن يكون فيه ضلعان متقابلان متوازيين ومتطابقين وبما أن ميل يساوي ميل ويساوي فإن ولأن QR = ST = فإن إذن QRST متوازي أضلاع.
27) اكتب برهاناً إحداثياً للعبارة: إذا كان كل ضلعين متقابلين في الشكل الرباعي متطابقين فإنه متوازي أضلاع.
الحل:
المعطيات:
المطلوب: متوازي أضلاع ABCD.
البرهان:
إذن وحسب تعريف متوازي الأضلاع يكون ABCD متوازي أضلاع.
28) اكتب برهاناً إحداثياً للعبارة: إذا كانت إحدى زوايا متوازي الأضلاع قائمة فإن جميع زواياه قوائم.
الحل:
المعطيات: ABCD متوازي أضلاع، الزاوية قائمة.
المطلوب: الزوايا B, C, D قوائم.
البرهان:
ميل
ميل
ميل : غير معروف.
ميل : غير معروف.
لذلك
إذن، الزوايا D, C, B قوائم.
29) برهان: اكتب برهاناً حراً للنظرية 1.10
الحل:
- المعطيات:
- المطلوب: ABCD متوازي أضلاع.
- البرهان: ارسم لتشكل مثلثين.
وبما أن مجموع قياسات زوايا أي مثلث يساوي 180º فإن مجموع قياسات زوايا المثلثين يساوي 360º.
إذن .
وبما أن و
وبالتعويض .
إذن .
وبقسمة كلا الطرفين على 2 ينتج لذا فإن الزاويتين المتخالفتين متكاملتان و
وبالمثل .
إذن هاتان الزاويتان المتحالفتان متكاملتان و
إذن الأضلاع المتقابلة متوازية لذلك فالشكل ABCD متوازي أضلاع.
30) المنساخ: استعن بمعلومات الربط مع الحياة إلى اليمين والشكل أدناه.
الحل:
a) إذا كان فاكتب برهاناً حراً لإثبات أن .
الحل:
- المعطيات:
- المطلوب:
- البرهان: نعلم ان
إذن AC = CF حسب تعريف التطابق.
(حسب مسلمة جمع القطع المستقيمة) وبالتعويض يكون AB + BC = CD +DF وباستعمال التعويض مرة أخرى يكون AB + BC = AB + DF وحسب خاصية الطرح BC = DF إذن حسب تعريف التطابق و (حسب خاصية التعدي) وإذا كان كل ضلعين متقابلين لشكل رباعي متطابقين فإن الشكل الرباعي متوازي أضلاع إذن BCDE متوازي أضلاع ومن تعريف متوازي الأضلاع يكون .
b) مقياس الرسم للشكل المنسوخ بالنسبة للشكل الأصلي هو نسبة CF إلى BE؟
فإذا كان AB = 12 in, DF = 8 in وطول الشكل الأصلي فما طول الشكل المنسوخ؟
الحل:
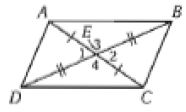
31) برهان: اكتب برهاناً ذا عمودين للنظرية 1.11
الحل:
المعطيات:
المطلوب: ABCD متوازي أضلاع.
العبارات (المبررات):
1) (معطيات).
2) (الزاويتان المتقابلتان بالرأس متطابقتان).
3)
4) (العناصر المتناظرة في المثلثين المتطابقين متطابقة).
5) ABCD متوازي أضلاع (إذا كان كل ضلعين متقابلين في شكل رباعي متطابقين فإنه متوازي أضلاع).
أوجد الإحداثيات المجهولة لرؤوس كل من متوازيي الأضلاع الآتيين:
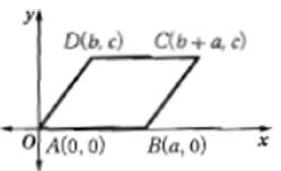
32)
الحل:
C (a, c)، D (-b, c)
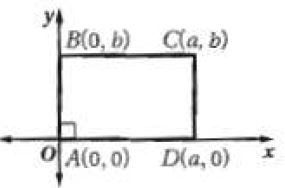
33)
الحل:
Y(a-b, c), X (a, 0)
34) برهان: اكتب برهاناً إحداثياً لإثبات أن القطع المستقيمة الواصلة بين منتصف أضلاع أي شكل رباعي تشكل متوازي أضلاع.
الحل:
المعطيات: RSTV شكل رباعي
والنقاط A, B, C، D متصفات الأضلاع على الترتيب.
المطلوب: ABCD متوازي أضلاع.
البرهان:
ارسم الشكل الرباعي RSTV في المستوي الإحداثي وسم الإحداثيات كما هو مبين في الشكل (استعمال إحداثيات من مضاعفات العدد 2 سيجعل الحسابات أسهل) ومن صيغة نقطة المنتصف تكون إحداثيات النقاط A,B,C,D هي:
ولأن ميلي متساويان فإن القطعتين المستقيمتين متوازيتين.
استعمل صيغة المسافة بين نقطتين لإيجاد
إذن لذلك ABCD متوازي أضلاع لأنه إذا كان ضلعان متقابلان في شكل رباعي متوازيين ومتطابقين فإنه متوازي أضلاع.
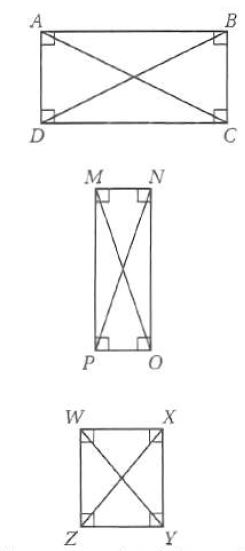
35) تمثيلات متعددة: في هذه المسألة سوف تستقصي احدى خصائص المستطيل.
a) هندسياً: ارسم ثلاثة مستطيلات بأبعاد مختلفة وسمها ABCD, MNOP, WXYZ ثم ارسم قطري كل منها.
الحل:
b) قس طولي قطري كل مستطيل ثم أكمل الجدول المجاور.
|
المستطيل |
القطر |
الطول |
|
ABCD |
AC |
|
|
BD |
||
|
MNOP |
MO |
|
|
NP |
||
|
WXYZ |
WX |
|
|
XZ |
c) لفظياً: اكتب تخميناً حول قطري المستطيل.
الحل: قطرا المستطيل متطابقان.
حلول أسئلة الثانوية مقررات
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
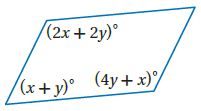

.JPG)
.JPG)
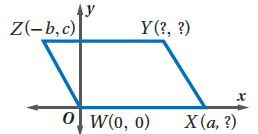

.JPG)







النقاشات