اختبار الفصل
أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعين المحدبين الآتيين:
1) السداسي.
n=6
720°=180°.(4)=180°.(6-2)=180°.(n-2)
2) ذو 16 ضلعاً.
n=16
2520°=180°.(14)=180°.(16-2)=180°.(n-2)
3) فن: تصنع جمانة إطاراً لتبسط عليه قطعة قماش وترسم عليها بألوان زيتية، ثبتت جمانة أربع قطع من الخشب بعضها ببعض
واعتقدت أنها ستمثل مربعاً.
a) كيف يمكنها التحقق من أن الإطار مربع؟
إذا كانت الزوايا الأربعة قائمة فإن الشكل مستطيل، وإذا كانت الأضلاع المتتالية متطابقة فإن الشكل معين، وحسب النظرية 1.20 بما أن الشكل مستطيل ومعين فإنه مربع.
b) إذا كانت أبعاد الإطار كما في الشكل، فأوجد القياسات المجهولة.
بما أن أضلاع المربع الأربعة متساوية الطول فإن x=2 ft
وبما أن زوايا المربع الأربعة قائمة فإن y=90°
الشكل الرباعي ABCD شبه منحرف متطابق الساقين.
4) ما الزاوية التي تطابق ؟
حسب النظرية 1.21 إذا كان شبه المنحرف متطابق الساقين، فإن زاويتي كل قاعدة متطابقتان.
5) ما الضلع الذي يوازي ؟
حسب تعريف شبه المنحرف يكون:
6) ما القطعة المستقيمة التي تطابق ؟
حسب نظرية 1.23 يكون شبه المنحرف متطابق الساقين، إذا وفقط إذا كان قطراه متطابقين.
وبالتالي فإن:
أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه في كل مما يأتي:
7) 900
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 900 هو حل المعادلة:
بما أن n=7 إذاً للمضلع 7 أضلاع.
8) 1890
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 1890 هو حل المعادلة:
بما أن n=13 إذاً للمضلع 13 ضلع.
9) 2880
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 2880 هو حل المعادلة:
بما أن n=18 إذاً للمضلع 18 ضلع.
10) 5400
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 5400 هو حل المعادلة:
بما أن n=32 إذاً للمضلع 32 ضلع.
11) اختيار من متعدد: إذا كان QRST متوازي الأضلاع، فما قيمة x؟
- 11
- 12
- 13
- 14
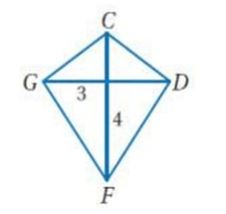
إذا كان CDFG على شكل طائرة ورقية فأوجد القياس المطلوب في كل من السؤالين الآتيين:
12) GF
بما أن قطري شكل الطائرة الورقية متعامدان فإنهما يقسمانه إلى أربعة مثلثات قائمة الزاوية.
نستعمل نظرية فيثاغورس لإيجاد GF:
13)
بما أن الشكل طائرة ورقية فإنه حسب النظرية 1.26 يكون ، وبما أن الطائرة الورقية لها أربعة أضلاع، فإن مجموع قياسات زواياه الداخلية 360:
جبر: استعن بالمعين MNOP للإجابة عن الأسئلة الآتية:
14)
بما أن قطرا المعين متعامدان فإن المثلث قائم وبالتالي فإن:
15) إذا كان 12 = PR، فأوجد RN.
قطرا المعين ينصف كل منهما الآخر: RN=PR=12
16) إذا كان 124 = ، فأوجد .
كل قطر في المعين ينصف الزاويتين اللتين يصل بين رأسيهما وبالتالي:
17) إنشاءات: تبني عائلة صالح ملحقاً للمنزل، وتركت فتحة لنافذة جديدة. فإذا قاس صالح الأضلاع المتقابلة فوجدها متطابقة. وقاس القطرين فوجدهما متطابقين، فهل يمكنه القول: إن فتحة النافذة تمثل مستطيلاً؟ وضح إجابتك.
نعم فتحة النافذة تمثل مستطيلاً، في الشكل الرباعي إذا كان كل ضلعين متقابلين متطابقان فإن الشكل الرباعي متوازي أضلاع، وإذا كان قطرا متوازي الأضلاع متطابقان فإنه مستطيل.
استعمل المبين جانباً لإيجاد كل مما يأتي:
18)
كل زاويتين متقابلتين في متوازي الأضلاع متطابقتان (النظرية 1.4)
19) JK
كل ضلعين متقابلين في متوازي الأضلاع متطابقان (النظرية 1.3)
JK=ML=6
20)
كل زاويتين متحالفتين في متوازي الأضلاع متكاملتان (النظرية 1.5)
جبر: استعن بالمستطيل DEFG للإجابة عن الأسئلة التالية:
21) إذا كان ، فاوجد EG.
لإيجاد EG نوجد قيمة x:
لحساب EG نعوض قيمة x=9:
22) إذا كان ، فأوجد .
نوجد قيمة x:
نعوض قيمة x=5:
23) إذا كان ، فأوجد GF.
نوجد قيمة x:
نعوض قيمة x=10:
حدد ما إذا كان الشكل الرباعي متوازي أضلاع أم لا في كل مما يأتي. برر إجابتك.
24) .JPG)
نعم الشكل الرباعي متوازي أضلاع لأن كل زاويتين متقابلتين متطابقتان. (النظرية 1.9)
25) 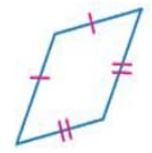
الشكل الرباعي ليس متوازي أضلاع لأنه لا يحقق أي شرط من شروط متوازي الأضلاع.
حلول أسئلة الثانوية مقررات
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)




النقاشات